Em sua essência, um conjunto é uma coleção de objetos únicos.


A Teoria dos Conjuntos é uma ferramenta versátil, presente em diversas áreas do conhecimento, desde a matemática pura até aplicações práticas em ciências e engenharia. Aqui estão algumas das aplicações mais comuns:
É habitual usar letras maiúsculas para dar nomes aos conjuntos, como A, B, C, D etc. e representar seus elementos por letras minúsculas, como [a, b, c, d] etc.
Veja as três principais formas de representar um conjunto:
Na representação tabular de um conjunto, os elementos são representados entre chave e separados por vírgula ou por ponto e vírgula.
a) A = {segunda, terça, quarta, quinta, sexta, sábado, domingo}
b) B = {0, 2, 4, 6, 8, 10}
c) C = {1,75; 1,81; 1,79; 1,82; 1,70}
Obs.: Na forma tabular, usa-se ponto e virgula na separação de número decimais, como no conjunto C dos exemplos, pois a vírgula poderia ser confundida com a vírgula que separa as casas decimais de cada número.
A representação de um conjunto por um diagrama de Venn (John Venn, 1834-1923) é aquela em que os elementos são simbolizados por pontos interiores a uma região plana, delimitada por uma linha fechada que não se entrelaça.
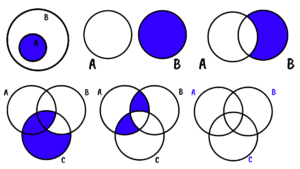
Nessa representação, os elementos de um conjunto A são descritos por meio de uma propriedade que os determina. Assim podemos representar um conjunto A por:
A = {x|x tem a propriedade p}
Obs.: lemos “A é conjunto de todos os elementos x, tal que x tem a propriedade p”
a) A = {x|x é um país da América do Sul}
Ou seja: O conjunto A é formado por todos os países da América do Sul.
b) B = {x|x é um planeta do Sistema Solar}
Ou seja: O conjunto B é formado por todos os planetas do Sistema Solar.
c) C = {x|x é um número primo}
Ou seja: O conjunto C é formado por todos os números primos.
Conjunto unitário: é aquele formado por um único elemento.
O conjunto A é unitário, pois é formado apenas por um único elemento, isto é, A={3}
Conjunto vazio: é aquele que não possui elemento algum. Representa-se o conjunto vazio por Ø ou { }.
O conjunto B é vazio, pois, como não existe número que satisfaça essa condição, B não possui elemento algum, isto é, B=Ø
Conjunto finito: Um conjunto é finito se for vazio ou se, ao contar seus elementos um a um, chega-se ao fim da contagem.
a) O conjunto A={a, b, c, d, e, f} é um conjunto finito, pois podemos contar seus elementos e chegar ao fim da contagem.
b) O conjunto B={x|x é pessoa brasileira} é um conjunto finito, pois podemos contar seus elementos e chegar ao fim da contagem.
c) O conjunto C=Ø é um conjunto finito, pois é vazio.
Conjunto infinito: é todo conjunto que não é finito.
a) O conjunto dos números naturais: ℕ={0,1,2,3,4,…} é um importante conjunto infinito
b) Outro importante conjunto infinito é o conjunto dos números inteiros: ℤ={…,-3,-2,-1,0,1,2,3,…}
Conjunto universo: é aquele ao qual pertencem todos os elementos relacionados a esse estudo.
Obs.: O conjunto universo é representado por U.
a) Quando estudamos métodos de contagem, o conjunto universo é U={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …}
b) No estudo das figuras geométricas planas, como conjuntos de pontos, o conjunto universo é o plano.
c) No estudo das figuras geométricas espaciais, como conjunto de pontos, o conjunto universo é o espaço tridimensional.
Subconjunto: um conjunto B é subconjunto de um conjunto A quando seus elementos estão contidos em A.
a) A={2, 5, 3, 8, 9} e B={2, 5, 3}. Note que {2, 5, 3} ⊂ {2, 5, 3, 8, 9}
B ⊂ A (lemos: “B está contido em A“)
b) B={2, 5, 3} e C={2, 5, 3}. Note que {2, 5, 3} ⊂ {2, 5, 3}
B ⊂ C (lemos: “B está contido em C“)
c) B={2, 5, 3} e D={2, 5, 7, 9}. Note que {2, 5, 3} ⊄ {2, 5, 7, 9}
B ⊄ D (lemos: “B não está contido em D“)
P1. O conjunto vazio é subconjunto de qualquer conjunto.
∅ ⊂ A (para qualquer conjunto A)
P2. Todo conjunto é subconjunto de si mesmo.
A ⊂ A (para qualquer conjunto A)
N1.Outra forma de representar B ⊄ D é D ⊅ A (lemos: “D não contém B“).
Assim no exemplo c, anterior, poderíamos ter escrito {2, 5, 7, 9} ⊅ {2, 5, 3}.
N2. A relação de inclusão, ⊂, é usada apenas para relacionar um conjunto B com um conjunto A que contém B: B ⊂ A
Por exemplo:
{3} ⊂ {1, 2, 3} e seria incorreto: {3} ∈ {1, 2, 3}
N3. A relação de pertinência, ∈, é usada apenas para relacionar um elemento x com um conjunto A que possui x como elemento: x ∈ A.
3 ∈ {1, 2, 3} e seria incorreto: 3 ⊂ {1, 2, 3}
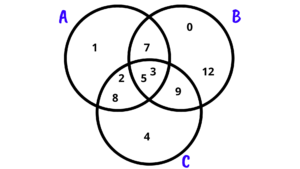
1. Represente na forma tabular cada um dos conjuntos A, B e C do diagrama abaixo.
2. Represente cada conjunto na forma tabular.
a) A = {x ∈ ℤ | x² = 9}
b) B = {x ∈ ℤ | x² ≥ 0}
c) C = {x ∈ ℤ | x² > 0}
d) D = {x ∈ ℤ | x² ≤ 0}
e) E = {x ∈ ℤ | x² < 0}
f) F = {x ∈ ℤ | (1/x) = 0}
g) G = {x ∈ ℕ | 56 < x ≤ 118}
h) H = {x ∈ ℤ | x < 0}
i) I = {x ∈ ℕ | x ≥ 70}
3. Classifique como finito ou infinito cada um dos conjuntos a seguir.
a) A = {x ∈ ℕ | x < 5}
b) B = {x ∈ ℤ | x < 5}
c) C = {x ∈ ℤ | x² = 9}
d) D = {x ∈ ℤ | x·0 = 0}
e) E = {x ∈ ℕ | x·0 = x}
4. Represente por meio de uma propriedade o conjunto A = {3, 5, 7, 9, …}.
5. Faça uma lista com todos os subconjunto de A = {1, 2, 3}