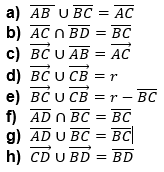Matemática – Teoria dos Conjuntos → Aula 01 – União e Intersecção de conjuntos - GECON

Aula 01 – União e Intersecção de conjuntos

RECONHECER

Definição

Uma operação de conjuntos é uma ação matemática que é aplicada a dois ou mais conjuntos para produzir um novo conjunto com base em regras específicas.

União (ou soma): A união de dois conjuntos A e B, denotada por $A \cup B$ , é o conjunto que contém todos os elementos que estão em pelo menos um dos conjuntos A ou B, ou em ambos.
Intersecção (ou produto): A intersecção de dois conjuntos A e B, denotada por $A \cap B$ , é o conjunto que contém todos os elementos que estão em ambos os conjuntos A e B.

Exemplo

Compras em uma Loja

Suponha que você tem dois conjuntos de itens comprados em uma loja:

$B = {laranjas, uvas, peras}$

A união dos conjuntos A e B representa todos os itens comprados, sem duplicatas:

$A \cup B = {maçãs, bananas, laranjas, uvas, peras}$

A intersecção dos conjuntos A e B representa os itens que são comuns em ambas as compras:

$A \cap B = {laranjas}$

RELACIONAR

Aplicações da União e Intersecção de Conjuntos

A teoria dos conjuntos é uma área fundamental da matemática que estuda as propriedades e relações entre conjuntos de elementos. A união e a intersecção são operações básicas que podem ser aplicadas de diversas maneiras em diferentes contextos. Abaixo, destacam-se algumas aplicações importantes dessas operações:

1. Teoria de Probabilidade:

A união de eventos é usada para calcular a probabilidade de pelo menos um dos eventos ocorrer.
A intersecção de eventos é usada para calcular a probabilidade de ambos os eventos ocorrerem simultaneamente.

2. Banco de Dados:

Na consulta de bancos de dados, a união de conjuntos é usada para combinar resultados de várias consultas.
A intersecção de conjuntos é usada para encontrar registros comuns entre diferentes conjuntos de dados.

3. Lógica Booleana:

Na lógica booleana, a união de conjuntos representa a operação OR (ou), onde o resultado é verdadeiro se pelo menos um dos conjuntos é verdadeiro.
A intersecção de conjuntos representa a operação AND (e), onde o resultado é verdadeiro apenas se ambos os conjuntos são verdadeiros.

4. Geometria:

Na geometria, a união de conjuntos pode ser usada para representar a combinação de diferentes regiões em um plano.
A intersecção de conjuntos pode ser usada para representar a área comum entre duas ou mais regiões.

5. Conjuntos Disjuntos:

A união de conjuntos é útil para identificar a totalidade dos elementos em conjuntos disjuntos.
A intersecção de conjuntos em conjuntos disjuntos resultará em um conjunto vazio, já que não há elementos em comum.

6. Teoria dos Conjuntos em Programação:

Na programação, a união e a intersecção de conjuntos são frequentemente usadas para manipular e comparar coleções de dados.
Essas operações são úteis para filtrar dados, encontrar elementos comuns entre conjuntos e muito mais.

7. Análise de Circuitos Elétricos:

Na análise de circuitos elétricos, a união de conjuntos pode representar a combinação de diferentes caminhos para a corrente elétrica.
A intersecção de conjuntos pode ser usada para identificar pontos comuns entre diferentes partes do circuito.

As operações de união e intersecção de conjuntos são fundamentais em várias áreas da matemática, ciência da computação, engenharia e muito mais. Seja na teoria de probabilidade, lógica booleana, análise de dados ou qualquer outra disciplina, compreender e aplicar essas operações é essencial para resolver problemas e analisar relações entre conjuntos de elementos.

ASSIMILAR

União (ou reunião) de conjuntos

A união de dois conjuntos A e B, é indicada por A ∪ B, é o conjunto cujos elementos são todos aqueles que pertencem a A ou a B.

A ∪ B = {x | x ∈ A ou x ∈ B}

Lemos A ∪ B como “A união B”

Exemplos

a) Sendo A = {1, 2, 3} e B = {4}, temos: A ∪ B = {1, 2, 3 , 4}

b) Sendo C = {1, 2, 3 , 4} e D {4, 5}, temos: C ∪ D = {1, 2, 3 , 4, 5}

c) sendo E = {8, 9, 10} e F = {2, 3, 4, 5, 6, 7}, temos: E ∪ F = {2, 3, 4, 5, 6, 7, 8, 9, 10}

Representação da união de conjuntos por diagramas de Venn

Propriedades da união de conjuntos

Sendo A, B e C conjuntos quaisquer, termos:

P1. Se B é subconjunto de A, então A ∪ B = A. Se A ∪ B = A, então B é subconjunto de A. Ou seja: B ⊂ A ⇔ A ∪ B = A

Obs.: Como consequência da propriedade P1, temos:

Ø ∪ A = A e A ∪ A = A

P2. A ∪ B = B ∪ A

P3. (A ∪ B) ∪ C = A ∪ (B ∪ A)

Obs.: Como consequência da propriedade P3, a união de mais de dois conjuntos A1, A2, A3, …, An pode ser definida da seguinte maneira:

A1 ∪ A2 ∪ A3 ∪ … ∪ An = {x | x ∈ A1 ou x ∈ A2 ou x ∈ A3 ou … ou x ∈ An

Intersecção de conjuntos

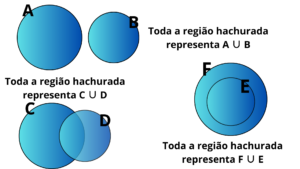
A intersecção de dois conjuntos, A e B, que indicamos por A ∩ B, é o conjunto cujos elementos são todos aqueles que pertencem a A e a B.

A ∩ B = {x | x ∈ A e x ∈ B}

Lemos A ∩ B como “A intersecção B“.

Exemplos

a) Sendo A = {1, 2, 3, 4} e B = {3, 4, 5, 6}, temos: A ∩ B = {3, 4}

b) Sendo C = {5, 6, 7} e D = {8, 9}, temos: C ∩ D = Ø

Nesse caso, os conjuntos C e D são disjuntos.

c) Sendo E = {b, c, d, e} e F = {a, b, c, d, e, f}, temos: E ∩ F = {b, c, d, e}

Representação da intersecção de conjuntos por diagramas de Venn

Propriedades da intersecção de conjuntos

Sendo A, B e C conjuntos quaisquer, temos:

P1. Se B é subconjunto de A, então A ∩ B = B. Se A ∩ B = B, então B é subconjunto de A. Ou seja: B ⊂ A ⇔ A ⊂ B = B

obs.: Com consequência da propriedade P1, vem:

Ø ∩ A = Ø e A ∩ A = A

P2. A ∩ B = B ∩ A

P3. ( A ∩ B) ∩ C = A ∩ (B ∩ C)

Obs.: como consequência da propriedade P3, a intersecção de mais de dois conjuntos A1, A2, A3, …, An pode ser definida da seguinte maneira:

A1 ∩ A2 ∩ A3 ∩ … ∩ An = {x | x ∈ A1 e x ∈ A2 e x ∈ A3 e … e x ∈ An}

P4. Propriedade distributiva da intersecção em relação à união:

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

P5. Propriedade distributiva da união em relação à intersecção:

A ∩ (B ∪ C) = (A ∩ B) ∩ (A ∩ C)

APLICAR

Exercícios Propostos

1.São dados os conjuntos:

A = {x ∈ $\mathbb {Z}$ | -4 < x ≤ 2}
B = [{ x ∈ $\mathbb {N}$ | x ≤ 3}
C = {x ∈ $\mathbb {Z}$ | -2 < x < 5}
D = {x ∈ $\mathbb {Z}$ | 3 ≤ x ≤ 8}

Determine:

a) A ∪ B

b) A ∩ B

c) A ∪ D

d) A ∩ D

e) A ∪ B ∪ D

f) A ∩ B ∩ C

g) A ∩ B ∩ C ∩ D

h) (A ∪ D) ∩ (B ∪ C)

i) (A ∩ D) ∪ ( B ∪ C)

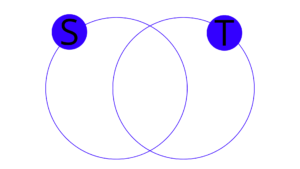
2. Sabendo que S ∩ T = {a, b, c, d} e S ∪ T = { a, b, c, d, e, f, g}, represente no diagrama abaixo os conjuntos S e T.

3. Sabendo que A ∩ B = {2, 5}, B = {2, 5, 9} e A ∪ B = {2, 3, 5, 8, 9}, represente os conjuntos A e B por meio de um diagrama.

4. Represente os conjuntos A = {1, 2, 3, 5, 12}, B = { 1, 2, 7, 8, 9} e C = {2, 4, 5, 8, 9} por meio de um diagrama.

5. cada um dos amigos Igor, Carla, Tiago, Janice e Leandro toca pelo menos um dos instrumentos: Piano ou violão ou saxofone.

Apenas Ígor e Carla tocam os três instrumentos.
Tiago toca piano e violão.
Janice toca violão e saxofone.
Leandro toca apenas piano.

Considere esse grupo de amigos e represente na forma tabular:

a) o conjunto das pessoas que tocam piano ou violão.

b) o conjunto das pessoas que tocam piano e violão.

c) o conjunto das pessoas que tocam apenas saxofone.

5. Se A, B, C, D e F são conjuntos quaisquer tais que A ∩ B = D e A ∩ C = F, então o conjunto A ∩ (B ∪ C) é igual a:

a) D ∩ F

b) D ∪ F

c) D

f) F

e) Ø

6. A figura a seguir apresenta quatro pontos distintos, A, B, C e D, pertencentes a uma reta r.

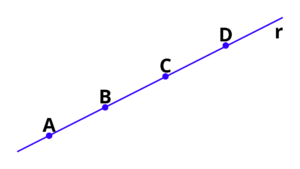
Classifique como verdadeira (V) ou Falsa (F) cada afirmação a seguir.

Referências

Paiva, Manoel Rodrigues – Matemática: Paiva / Manoel Rodrigues Paiva. – 2. ed. – São Paulo: Moderna, 2010.
Dante, Luiz Roberto – Matemática, volume único: livro do professor / Luiz Roberto Dante. – – 1. ed. – – São Paulo: Ática, 2005.